Inside Magma: How the Russian GOST R 34.12-2015 block cipher works

The “Magma” algorithm is essentially an exact copy of the block cipher from the old GOST 28147-89, with one key difference. In the newer GOST 34.12-2015, the substitution boxes (S-boxes) for the nonlinear bijective transformation are explicitly defined and fixed, whereas in GOST 28147-89 they were not specified and implementers were free to choose their own S-box values.

In theory, if you define the S-box yourself and keep it secret, you can improve the cipher’s strength (it effectively increases the key size). However, as we can see, the authors of GOST 34.12–2015 chose to take that flexibility away from users.

As noted earlier, the Magma cipher uses a 64-bit block size and a 256-bit encryption key.

A bit of theory

In the algorithm described, the 64-bit block to be encrypted is split into two equal 32-bit halves—right and left. Then 32 rounds are performed using round keys derived from the original 256-bit encryption key.

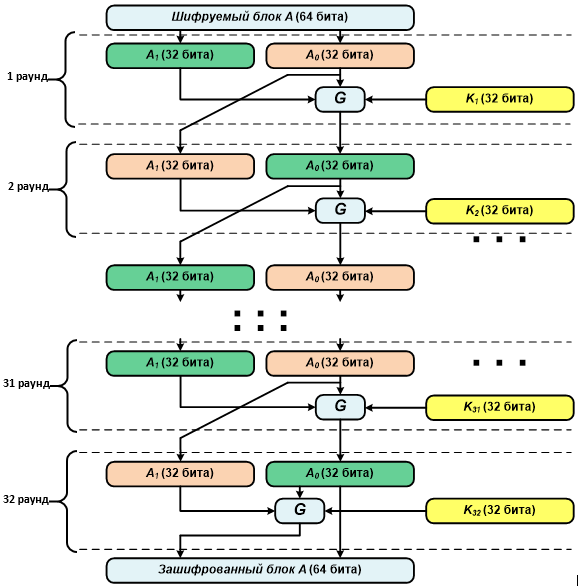
In each round (except the thirty-second), a Feistel-based transformation is applied to the block’s right and left halves. First, the right half is added to the current round key modulo 2^32. The resulting 32-bit value is split into eight 4-bit chunks, and each chunk is substituted via an S-box (previously referred to as a nonlinear bijective transformation). The result is then rotated left by 11 bits and XORed with the left half. The resulting 32-bit value becomes the new right half, while the previous right half is moved to the left half.

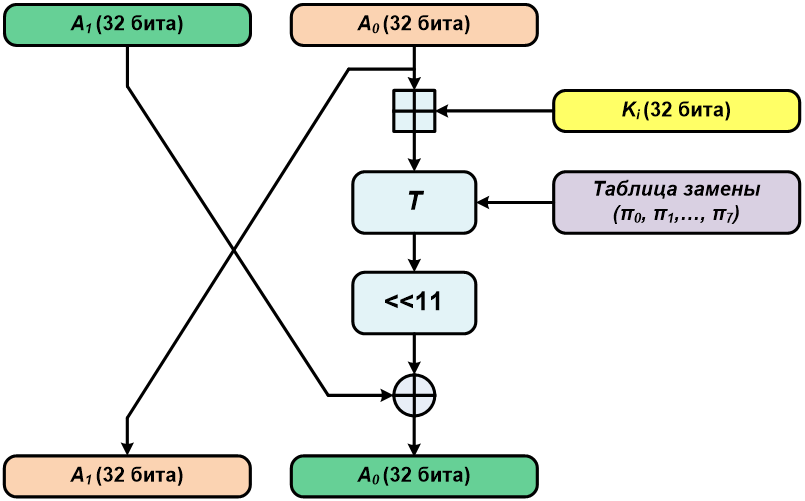
In the final (thirty-second) round, the right half is processed as described above; the result is written into the left half of the original block, while the right half remains unchanged.

The round keys are derived from a 256-bit master key. The master key is split into eight 32-bit subkeys, which are applied in this order: three passes from the first through the eighth, and one pass from the eighth back to the first.

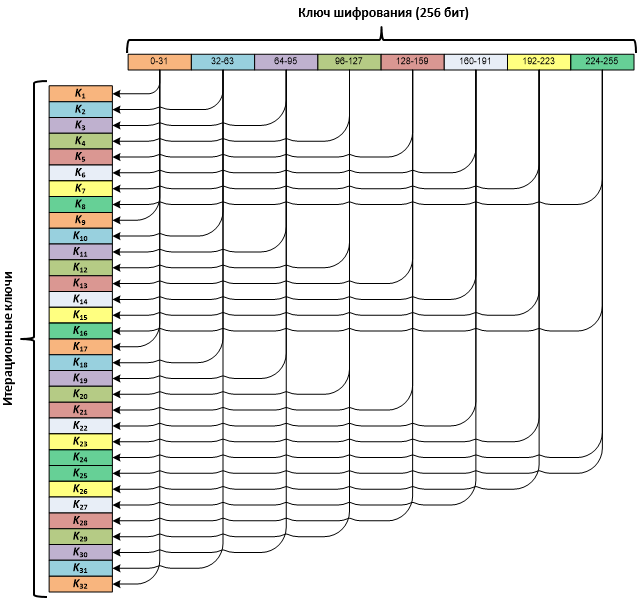
For decryption, the same sequence of iterations is used as for encryption, but the keys are applied in reverse order.

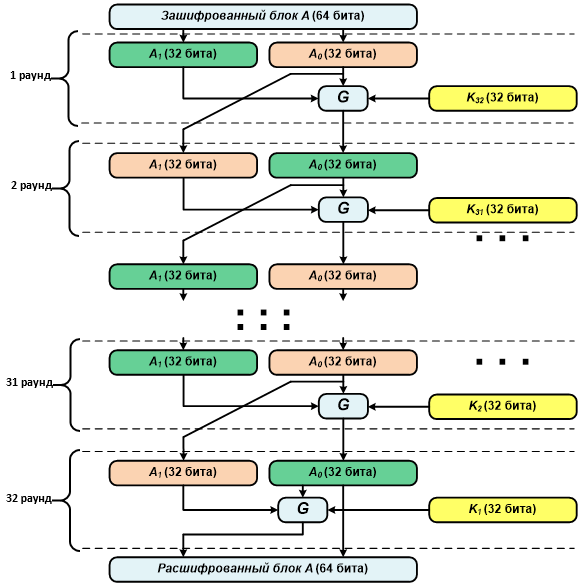
With a quick theoretical primer out of the way, let’s start coding.

Core functions of the standard

Since the algorithm operates on 32-bit blocks (as so-called binary vectors), let’s start by defining this block:

Bitwise XOR of Two Binary Vectors

Each byte of the first vector is XORed with the corresponding byte of the second vector, and the result is written to a third (output) vector:

Addition of Two Binary Vectors Modulo 2^32

This function is analogous to the “addition in the ring of residues modulo 2^n” used in the Streebog algorithm, except that here n is 32 rather than 512 as in the Streebog standard. The two input 4-byte vectors are treated as 32-bit integers and added; any overflow, if it occurs, is discarded:

Nonlinear bijective transformation (T‑transformation)

Unlike the Streebog and Kuznyechik algorithms (there, this step is called the S-transformation/S-box), a different substitution table is used here.

Because in the standard’s text (by some obscure convention) byte 0 is listed last and the final byte first, the program will only work correctly if you write the table rows in reverse order—rather than as described in the standard.

The code for the T transformation function ends up looking like this:

Key schedule

As noted earlier, encryption and decryption require thirty-two 32-bit round keys derived from the original 256-bit key.

First, let’s decide where the retrieved key values will be stored:

After that, you can proceed with the actual deployment of the keys:

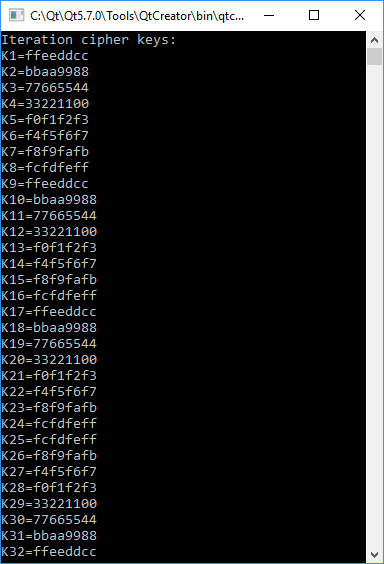
Sure, you could write all of this using loops, but here the function is implemented in a straightforward, straight-line way for clarity, and theoretically it should be faster in this form.

The g Transformation

The transformation includes adding the right half of the block to the round key modulo 2^32, applying a nonlinear bijective substitution (S-box), and rotating left by eleven bits:

G-Transformation

This transformation represents a single round of the encryption or decryption cycle (from the first through the thirty-first). It includes applying the g transformation, XORing (addition modulo 2) the result of g with the right half of the block, and swapping the contents of the left and right halves of the block.

Final G Transformation

This is the final (thirty-second) round of encryption or decryption. Unlike the simple G transformation, it does not swap the values between the right and left halves of the input block:

Encrypting

As noted earlier, encryption runs for 32 iterations: rounds 1 through 31 use the G transformation, and round 32 uses the final G transformation:

Before calling this function, make sure to invoke GOST_Magma_ExpandKey to populate the round key array with the required values.

Decryption

Decryption is performed similarly to encryption, using the round keys in reverse order:

Also, don’t forget about GOST_Magma_ExpandKey, since decryption uses the same round keys as encryption.

Conclusion

The Magma cipher from GOST R 34.12-2015 is much simpler to implement than the Kuznyechik (Grasshopper) cipher from the same standard, and it is currently used far more widely (including in the GOST 28147-89 variant with S-boxes defined by implementers themselves or taken from RFC 4357).

You can now encrypt both 128-bit blocks (using Kuznyechik, aka Grasshopper) and 64-bit blocks (using Magma). Bulk-encryption procedures and modes of operation for these two ciphers—namely ECB (simple substitution), CTR (gamma), OFB (gamma with output feedback), CBC (simple substitution with chaining), CFB (gamma with ciphertext feedback), and MAC generation—are specified in a separate standard: GOST 34.13–2015 “Information technology. Cryptographic data security. Modes of operation of block ciphers.” More on this in upcoming articles.